Reflecting on Questioning
by Ed Nolan
How do you use questions to support your students?
Do your questions focus on what you hear from students or do you funnel students toward a particular strategy you feel is best for the students? Does it matter?
One way of thinking about teacher questioning is considering the difference between “focusing” and “funneling” (Herbal-Eisenmann & Breyfogle, 2005; Wood, 1998).
When student sense making guides teacher questioning provided in response to student contributions, the teacher is focusing on student thinking. This type of questioning allows for connections between what students provide in their answers and the goal the teacher has for the lesson. Here, both the teacher and the students are engaging in the cognitive activity of making sense of the problem and solution.
When teachers use funneling questions, they guide students toward a particular outcome within the lesson regardless of what the students provide. This often occurs when teachers are looking for a specific strategy that they want students to use and they accomplish this by asking questions and collecting responses from students until they hear the student contribution they seek. Sometimes teachers will start from a student’s incorrect response and ask a series of questions leading the student to the strategy they desire. Teachers may also use the funneling question structure to lead students through the steps of a procedure or process. In funneling, the teacher is the one engaging in the cognitive activity (Wood, 1998).
Let’s look at a hypothetical example to help understand the difference between the two: Imagine a lesson where the goal is to identify the slope of line segments from a graph. One way to begin this lesson might be to allow students to explore the slope of segments as sides of triangles on a coordinate grid (see below).
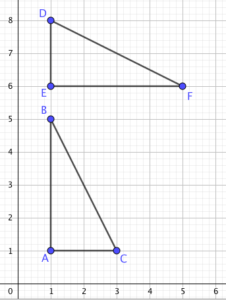
Exploring slope using triangles on a coordinate grid
Consider the following two classroom vignettes:
Vignette 1
Teacher: What do you notice about segments BC and DF?
Calvin: I see that the change for segment BC goes down 4 and over 2 and the change for DF goes down 2 and over 4, hey, that means they are the same…
Teacher: They cannot be the same, as one goes down 4 and the other goes down 2.
Calvin: No, I mean that the triangles are the same.
Teacher: But that is not what we are looking for, what about the vertical change compared to the horizontal change? How are they different?
Calvin: What do you mean?
Teacher: How do you explain the ratio between the vertical change and the horizontal change?
…
Vignette 2
Teacher: What do you notice about segments BC and DF?
Calvin: I see that the change for segment BC goes down 4 and over 2 and the change for DF goes down 2 and over 4, hey, that means they are the same…
Teacher: Explain more about what you mean.
Calvin: The triangles are the same.
Teacher: How do you know they are the same?
Calvin: I can see that they are both right triangles and ABC has sides that are 2 and 4 units long and so does DEF.
Teacher: That is interesting. And how do the relationships of the sides BC and DF compare to each other?
Calvin: They are the same length.
Teacher: And how do those lengths connect to how we can describe the ratio of the vertical change to the horizontal change?
…
In the first vignette, the teacher is working to guide the student to see the rate of change of the segments and is using “funneling” to direct students toward the desired outcomes of the lesson. Funneling allows the teacher to take control of the thinking of the lesson and may occur in exploration when time is pressing or when the teacher wants to direct students to think in the same way as the teacher. What is lost is the opportunity to value the students’ thinking and to connect the learning goal to what students provide during instruction.
In the second vignette, the teacher uses the student’s response and guides the thinking toward the learning goal. Notice how the teacher builds off of what the student has offered and guides the thinking of the student toward the learning goal. This can take more instructional time but it helps students make connections between their current reasoning and the learning goal.
Here you get a sense of some of the differences between the focusing and funneling question structures. Consider your own questioning:
What role do students’ responses play in your questioning?
How do you use questioning to learn more about students’ thinking, and how do you use questioning to guide your lesson?
How does your questioning in response to student contributions differ when your students are exploring a concept, linking the concept to a procedure, or practicing a procedure?
In examining your questioning, you are demonstrating how you value student thinking. It is a difficult task and requires you to make sense of mathematics for teaching, to adjust to student-provided strategies as a guide for the development of understanding. Listening carefully to students and building off of their ideas takes a great deal of energy – but the rewards are clear. Students are able to connect their current ideas to the new concepts and procedures we need them to understand, and they will remember them better. And you will find that in working to make sense of student thinking and developing questions that link student thinking to your instructional goal, you deepen your own understanding of mathematics!
I am interested in your reactions to this blog, as well as your own examples of funneling and focusing and how you use them in the classroom. Feel free to respond on Twitter and tag me (@ed_nolan) – include the hashtag #DNAmath or any of the grade level hashtags of #MSMTK2, #MSMT35, #MSMT68, or #MSMTHS to bring more mathematics educators into the conversation.
Herbal-Eisenmann, B. A., & Breyfogle, M. L. (2005). Questioning our “patterns” of questioning. Mathematics Teaching in the Middle School, 19(9), 484-489.
Wood, T. (1998). Alternate patterns of communication in mathematics classes: Funneling or focusing? In H. Steinbring, M. G. Bartolini Bussi, & A. Sierpinska (Eds.), Language and communication in the mathematics classroom (pp. 166-178). Reston, VA: National Council of Teachers of Mathematics.
