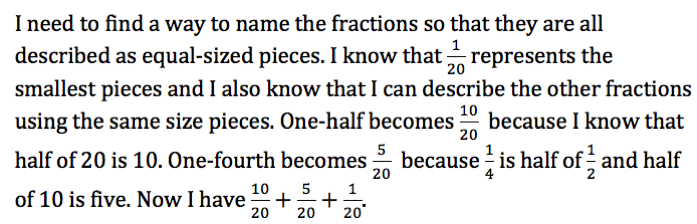The terms “explain” and “justify” are used frequently when discussing expectations for how students should support their solutions in mathematics. But what do we really mean? Is there a difference between explaining and justifying? I think there is a difference. To me, an explanation describes what the student did (frequently this is simply the steps taken to perform a procedure) and a justification includes why what the student did is mathematically okay. While this description is helpful, it isn’t enough. The purpose of this post is to make sense of that difference through the use of a mathematical task.
The terms “explain” and “justify” are used frequently when discussing expectations for how students should support their solutions in mathematics. But what do we really mean? Is there a difference between explaining and justifying? I think there is a difference. To me, an explanation describes what the student did (frequently this is simply the steps taken to perform a procedure) and a justification includes why what the student did is mathematically okay. While this description is helpful, it isn’t enough. The purpose of this post is to make sense of that difference through the use of a mathematical task.
Consider this task.
Two students are asked to compare 4/7 and 4/5 to determine which fraction is greater.
The students both conclude that 4/5 is greater than 4/7.
One student says that the numerators are the same so the denominators can be compared. Since five is less than seven, 4/5 is greater than 4/7.
Another student says that both fractions describe four parts of a whole. With 4/5 the whole is divided into fewer pieces than with 4/7. Since there are fewer pieces in the same-size whole, the pieces must be bigger. Therefore, 4/5 is greater than 4/7.
In both responses, the students provide a description of their thinking. However, only the second response provides a window into why the student’s thinking is mathematically valid. It is interesting to note that the explanation used the terms numerator and denominator while the justification did not include mathematical vocabulary. Students can provide justifications even if they do not have mastery of academic vocabulary. Students can reason in their own words. Reasoning is important. An explanation is provided without evidence of mathematical reasoning. A justification is based on mathematical reasoning.
In the fraction comparison example, the student’s explanation is fairly complete. You might be more likely to observe a student simply explain that the common numerator strategy was used without going into further detail. The explanation provided earlier includes a deeper description but it still does not include information regarding why the denominators can be compared so it is not a justification.
I believe that we should require students to justify their thinking as they build conceptual understanding. Once students transition from making sense of concepts to applying more efficient procedures, explanations of what they did should suffice, with the expectation that they can justify their thinking when asked. Since concepts should be taught before procedures then it follows that students would provide justifications for solutions to problems before they would provide explanations without justifications. This fits well with my position on academic vocabulary (see my earlier blog post below). Justifications do not rely on academic vocabulary – I would even go as far as to argue that withholding some academic vocabulary is useful in providing a justification. By avoiding the terms numerator and denominator with the fraction comparison problem, the second student needed to explain their meanings.
Justifications are time consuming to produce. Once students are comfortable justifying their thinking about a mathematical idea, the justification is no longer necessary. At this point, a simple explanation should suffice. Explanations are most efficient when they are provided through the use of academic vocabulary as in the example above where the student noted that with common numerators, one can simply compare the denominators.
There is a difference between explanations and justifications. Both are important, what matters is when they are emphasized. This is the case with many aspects of mathematics instruction.
Notice the trends and how they work together –
– We should teach concepts before procedures.
– We should support students to use everyday language before academic language.
– We should expect students to provide justifications before explanations.
How we organize our instruction influences how students come to make sense of mathematics. With this in mind, when do you think it makes sense to give students notes on mathematical ideas? This will be the topic of my next post.